Kiri's diary

きりねこNote

数学関連のことについてよく書きます

複素解析をざっとまとめるー5（様々な複素関数その1）

ざっと複素解析 複素解析論

目次

様々な複素関数

 

　様々な複素関数について勉強していきます. 内容は, 指数関数, 対数関数, 累乗関数, 三角関数です. 実数で定義されていたそれぞれの関数を複素数にまで拡張して, 実数の場合とどこが違うのか, どこが同じなのかを勉強しましょう.


複素関数について

　実関数と複素関数の違いについて話します.
　実1変数関数 y = f(x) の場合には, xy 平面の中にグラフを描く事ができました. なぜなら実数 x と実数 y の対応である関数の表現には2つのパラメーターで事足りるからです. 同様に実2変数関数 z=f(x,y) のグラフは x,y,z の3つのパラメーターがあれば表現できるので, 3次元の空間に描くことができます.しかし複素関数はそうはいきません.
　実1変数関数を y=f(x) と書くように, 複素1変数関数は w=f(z) と書くことが多いです. 複素1変数関数 w=f(z) のグラフを描くには複素数 w と複素数 z を表現するパラメーターが必要です. しかし1つの複素数を表現するには2つのパラメーターが必要です. 直交座標系なら実部と虚部, 極座標系なら原点からの距離 r と偏角 \theta です. つまり2つの複素数が含まれる w=f(z) のグラフを描くには4次元が必要となります.
　残念ながら私たちは4次元を認識することはできません(縦, 横, 高さに加えて, 《色》を用いて4次元を表現する方法はあります). なので, w=f(z) のグラフを表現するには, 複素平面を2つ用意します. 複素1変数関数は平面と平面の対応です. 関数 w=f(z) は, 複素数 z の複素平面と複素数 w の複素平面の対応ということになります. それぞれの複素平面を z 平面, w 平面と言います. これが実関数とのグラフの違いです. 1つの平面ないしは空間内にグラフを描けないため, 実関数に比べて関数を視覚的に捉えにくいこともあると思います.
　たとえば, w=f(z)=z^{2} という関数において z 平面上の複素数を z=1+ai\quad(\infty \lt a \lt \infty ) とすると z 平面から w 平面への写像 w=f(z) は次の図のようになります.

f:id:TeikaKiri:20180114161508p:plain

w=z^{2}

　しかし, それは逆に複素数のいいところでもあります. 1つの複素数を表すのに実部と虚部の2つのパラメーターが必要だからこそ, 複素平面を用いて幾何的に捉えることが可能です. たとえば, 実数 x に定義域として |x|\le 1 が与えられているとき, それを幾何的に捉えるには数直線の上で -1 と 1 に区切り線をつけるしかありません. 一方複素数 z に定義域として |z|\le 1 が与えられているとき, それは複素平面上で次の図ように表すことができます.

f:id:TeikaKiri:20180114161439p:plain

|z|\leq1

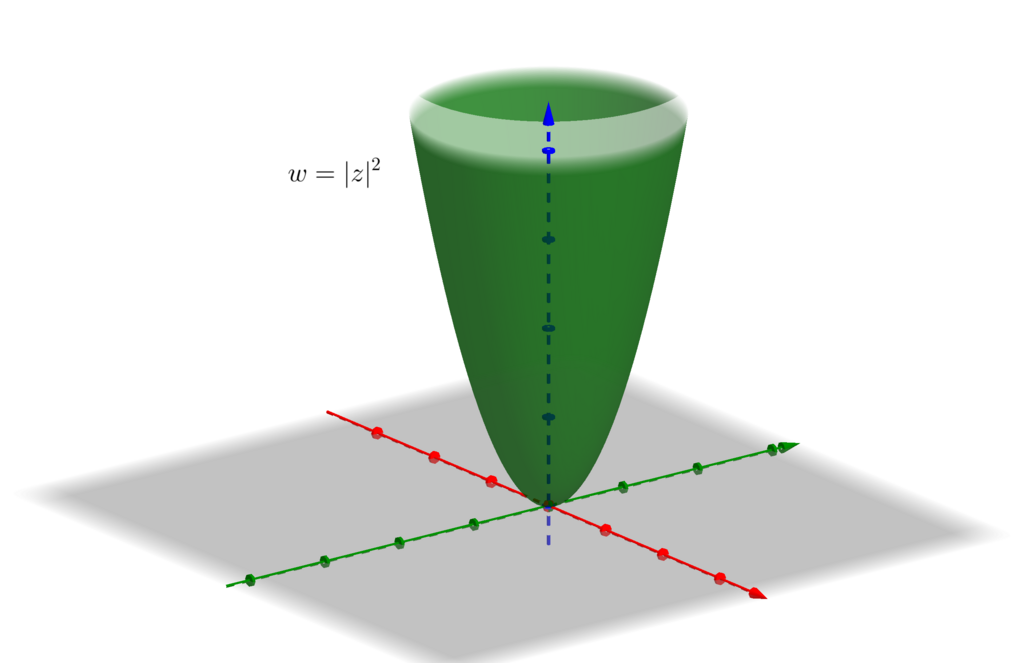
　先ほどの関数 w=z^{2} のように w が虚数の値も取りうる場合には z 平面と w 平面が必要でしたが, w が実数の値しか取らない場合には3次元空間にグラフを描くことが可能です(複素数 z に2つのパラメータ, 実数 w に1つのパラメータがあればよい). そのような関数として w=|z| や, w=|z|^{2} などがあります. このような絶対値の関数を絶対値曲面と呼びます. w=|z| と w=|z|^{2} のグラフは次の図のようになります. 灰色の部分の平面が z 平面となっています. また, w=|z|^{2} は回転放物面となっています.

f:id:TeikaKiri:20180114161456p:plain

w=|z|

f:id:TeikaKiri:20180114161502p:plain

w=|z|^{2}